Geometria Parametrica
Studio

Area dell'Ellisse o del Settore di Ellisse
L’ Area dell'Ellisse o di un Settore di Ellisse è facilmente calcolabile tramite la formula dell'integrale delle funzioni parametriche dell'ellisse indicate sotto. Qualunque libro si consulti in proposito, indica:
Area Ellisse = mq \(\pi\)
Il fatto è che l'angolo indicato con \(\;\pi \)è l'angolo della circonferenza di riferimento, da cui le formule parametriche x = q cosE e y = m sinE (con q > m semiassi) e non l'angolo dell'ellisse, il cui valore β - vedi Fig.1 - è semplicemente legato all'angolo della circonferenza di riferimento dalla formula:
\( \qquad \qquad \tan\beta=\frac{m}{q}\tan E\)
E' ovvio che nei valori 0° 90° 180° 270° 360° il valore di β e di E coincidono.
La dimostrazione di quanto detto è in Equazione di VAG nel Piano - Capitoli (Capitolo VII° - Area e Perimetro Ellisse - II° Integrale di VAG).
Qui ne diamo una sintetica illustrazione:
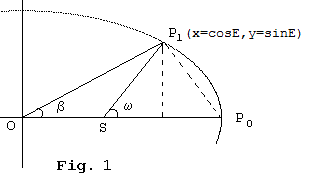
In una Ellisse - Fig. 1 - abbiamo che l'Area del Settore P0OP1P0 = S1 come risultato di un integrale dato in forma parametrica è:
\( \qquad \qquad S_1=\frac{qm}{2}E\)
con q > m semiassi ed E parametro (valore dell’angolo in radianti della circonferenza di riferimento), dove \(\tan\beta=\frac{m}{q}\tan E\) e per E = 2π si avrà l'area totale mq π come indicato all'inizio, mentre l’area P0SP1P0 = A1 vale:
\( \qquad \qquad A_1=\frac{qm}{2}E-\frac{OS\cdot y}{2}=\frac{qm}{2}E-\frac{OS \cdot m \sin E}{2}=\frac{qm}{2}\left(E-\frac{OS}{q}\sin E\right)\)
Pertanto abbiamo che: \( \quad \frac{S_1}{E}=\frac{A_1}{\left(E-\frac{OS}{q} \sin E \right)}=\frac{qm}{2}\quad \) dove l'area dell'ellisse, totale o parziale, rimane sempre proporzionale al valore dell'angolo E.
Posto \(\frac{OS}{q}=\epsilon\) poichè OS < q avremo ε < 1 e la formula generale per l'Area di un Settore di Ellisse, a partire dalla sua ascissa, è: \( \qquad S=\frac{qm}{2} \left(E-\epsilon sin E \right)\qquad \) dove:
- per ε = 0 avremo \(S_1=\frac{qm}{2}E\)
- per ε < 1 avremo \(A_1=\frac{qm}{2} \left(E-\epsilon sin E \right)\)
- per ε = 1 avremo \(P_0P_1P_0=\frac{qm}{2} \left(E- sin E \right)\)
Sia il punto A(x,y) di ellisse di semiassi q > m, che delimita l'area del relativo settore - vedi Grafico - avremo i valori parametrici di A [x = qcos(α) e y = msin(α)] da cui la relativa formula, dedotta dall'Integrale di VAG, in questo esempio grafico si intende α=E, entrambi angoli di riferimento di una circonferenza:
Area Settore PCAP = mq / 2*(α) con α in Rad
Area Parziale del Settore PBAP = mq / 2*[(α) - εsin(α)] con ε = CB / q
- Dare il valore dei semiassi q > m tramite gli Slider;
- Muovere il punto A fino ad indicare almeno una delle sue coordinate (in generale l'asse x): l'altra sarà data con arrotondamento ai decimali; aiutarsi con le frecce spostamento che variano di valori dell'ordine di 0,001;
- Trovate le coordinate di A, l'Area del Settore cercato è quello indicato con la prima formula;
- Spostando il punto B si ottiene l'Area parziale del Settore, con la seconda formula.
Qualora il punto B della Distanza CB coincidesse con il fuoco dell'ellisse si avrebbe che ε = e eccentricità: ed è in questo caso che rientra la Seconda Legge di Keplero, dove il valore \(\left(E-\epsilon sin E \right)=M \) è chiamato Anomalia Media ed E è detto Anomalia Eccentrica.
Ricordiamo l'importante relazione che intercorre tra i vari angoli, essendo l'angolo PBA=\(\omega\):
\(tan\beta=\frac{m}{q}tanE \); \(\;tan\omega=\frac{m sinE}{q(cosE-e)} \); \(\;sin\omega=\frac{m sinE}{q(1-e cos E)} \); \(\;cos\omega=\frac{cos E-e}{1-e cos E} \);
poiché per un valore di ε la formula della proprietà dell'ellisse dipende da E, angolo di una circonferenza, da cui è facile dedurre la costanza delle aree.
Si noti che nella formula che lega gli angoli, il valore dell’angolo β è sempre riferito ad un angolo adiacente all'asse delle x - vedi Grafico - ma tale condizione non vale per il valore E della circonferenza di riferimento, essendo questi proporzionale alla relativa area, ovunque essa si trovi.
Un valore di β intermedio, cioè non adiacente all'asse delle x, può essere calcolato solo per differenza.
Analogamente, noto S1 = Area di un Settore di Ellisse di semiassi dati, essendo tale area proporzionale all'angolo E, da questi posso risalire al valore dell'angolo β, ma tale angolo si intende dalla ascissa.
Per un'area intermedia posso arrivare a conoscere il valore β soltanto conoscendo almeno un punto dell'estremo del settore, che mi permetta il calcolo di β per differenza.