Geometria Parametrica
Studio
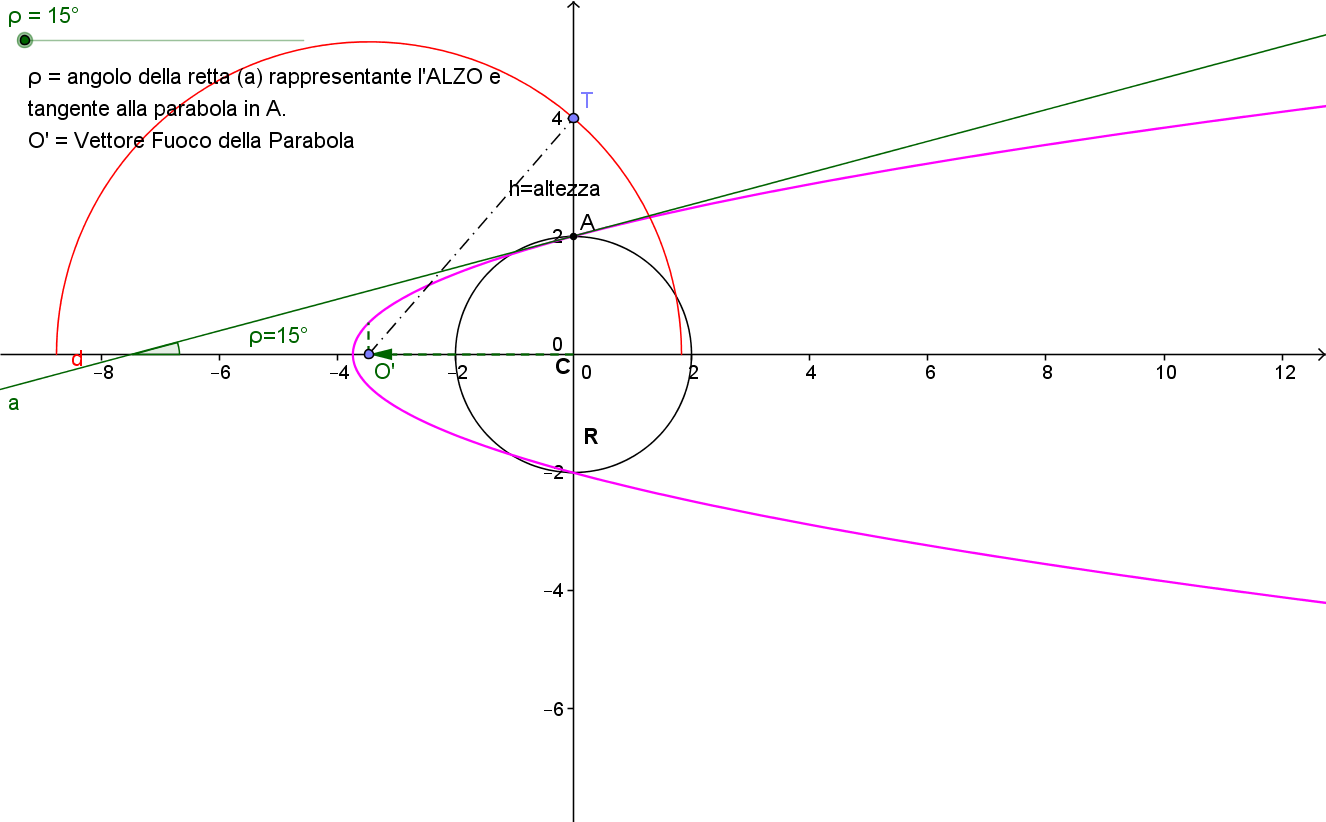
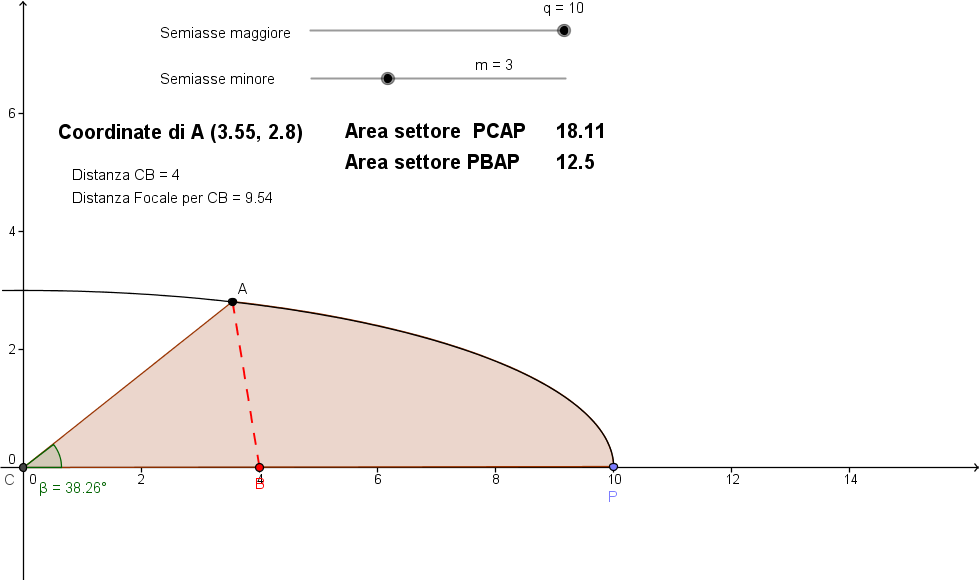
L'Equazione Parametrica di VAG
La Geometria con "L'equazione Parametrica di VAG" è la geometria che meglio rappresenta il valore delle distanze, e quindi delle figure, in funzione degli angoli. Essa è quella che meglio prende in considerazione le distanze e la loro posizione nello spazio e si rappresenta come due elementi divisi dal segno di uguaglianza dove una parte rappresenta la distanza nel suo valore assoluto nello spazio, nell'altra la sua collocazione secondo il riferimento scelto.
Il grande vantaggio nello Studio della Equazione Parametrica di VAG è nella estrema facilità di interpretazione e di descrizione, valutabili anche tramite semplici programmi al computer per cui ogni possibile curva è data dalla interpretazione che si dà alla Equazione Parametrica in questione.
Per una ricognizione della materia vedere Sguardo d'Insieme (Geometria)
Astronomia con la Geometria - Le Nuove Leggi
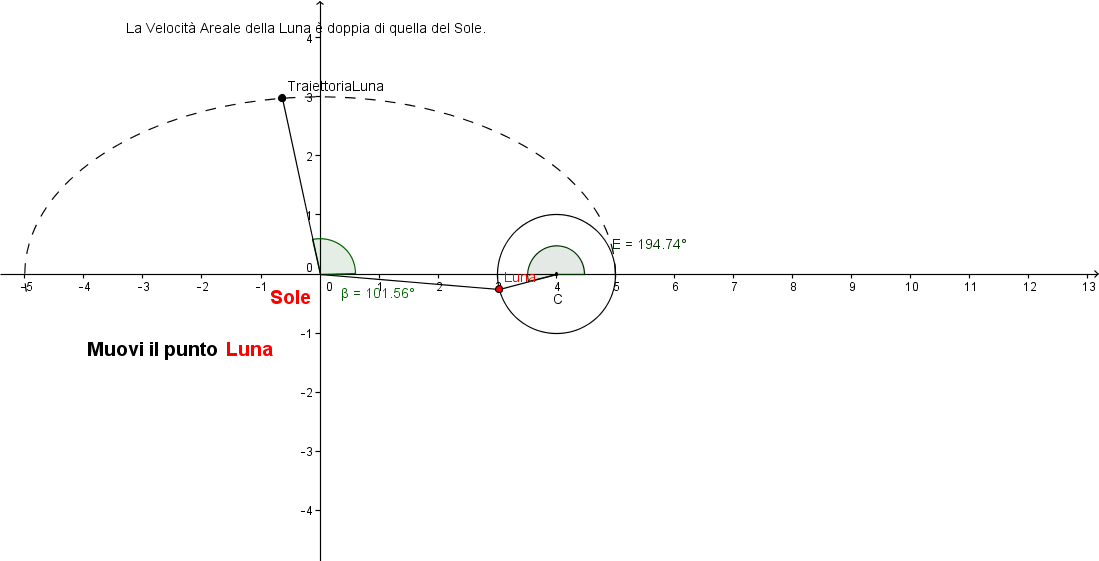
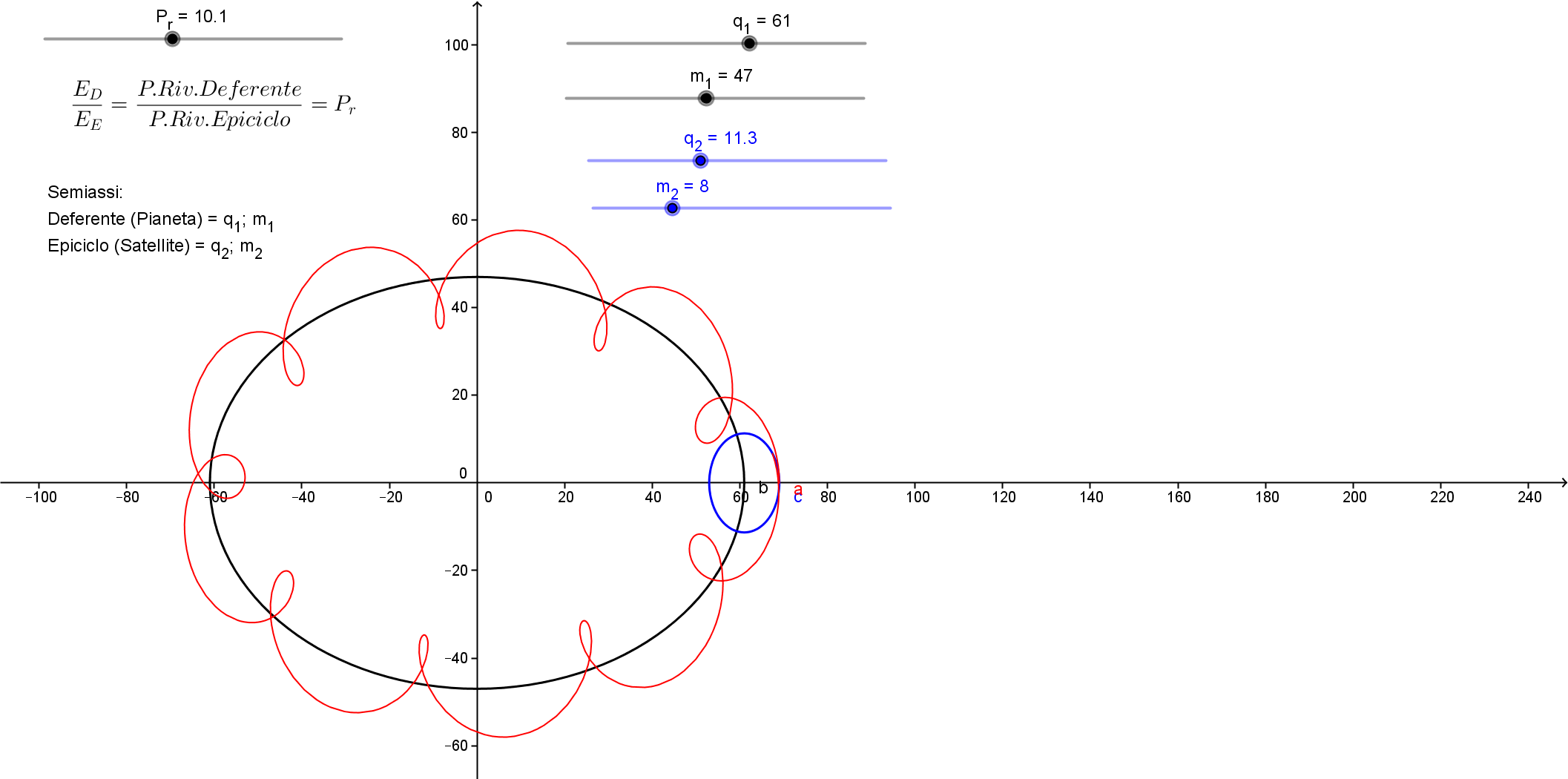
Per la prima volta i Moti Astronomici sono visti e interpretati con la Geometria Parametrica in quanto più vicina e migliore interprete della cinematica: tale geometria, infatti, interpreta la Velocità Areale, la costanza delle Aree e molte altre cose; tramite essa è possibile precisare senza approssimazioni i principi dell'Astronomia.
Come introduzione leggere: "L'Orologio di Tycho Brahe e le Leggi di Keplero"
Prima Legge del Moto dei Pianeti - Moto Orbitale
I Pianeti ruotano secondo proprie Orbite Circolari e tutti, uno rispetto all'altro, secondo traiettorie Ellittiche.
Considerazioni sulla Prima Legge sul Moto dei Pianeti
Seconda Legge del Moto nello Spazio - Moto Parabolico
Un corpo si sposta da un sistema ad un altro, secondo una curva parabolica (o Iperbolica) e ruota nel nuovo sistema secondo Orbite Circolari il cui centro è il fuoco della parabola.
