Geometria Parametrica
Studio

Considerazioni sulla Prima Legge sul Moto dei Pianeti
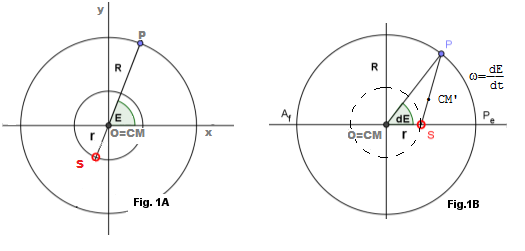
Il Moto di Rivoluzione e il Centro di Massa: in Fig.1A, nel Polo O sia il Centro di Massa CM di due corpi P ed S, di massa rispettivamente Pm e SM. Si ponga nel Polo il centro di un riferimento cartesiano ortogonale e si abbia la distanza \(\overline {SP}= R+ r \) con gli ultimi due termini dipendenti dall'anomalia E, uno con valore E e l'altro con valore (180+E), per cui sappiamo sussistere la relazione:
\(\quad P_m R =S_M r \); \(\;\; \frac{S_M}{P_m}=\frac{R}{r} \); \(\;\; \frac{S_M}{P_m+S_M}=\frac{R}{r+R} \)
ed essendo \(\;\; (R+ r)=SP \;\;\) avremo \(\;\; \frac {S_M}{P_m+S_M} \overline {SP}=R \;\;\) e \(\;\; \frac {P_m}{P_m+S_M} \overline {SP}=r \;\;\), la cui somma è appunto \(\;\; \overline {SP}=\vec R+\vec r \)
Nella Fig.1B - uguale alla Fig.1A - invece, sia la distanza \(\;\; \overline{SP}=\rho_1+\rho_2 \;\;\) distanze di un nuovo CM', posto sulla congiungente SP, per cui \(\;\; \rho_1P_m=\rho_2 S_M \;\;\) pertanto conoscendo le masse e la loro distanza SP, si ottiene quella relativa alle distanze di ciascuna massa dal punto CM' e con lo stesso procedimento visto in Fig.1A, abbiamo:
\(\quad \frac {S_M}{P_m+S_M} \overline {SP}=\rho_1 \;\;\) e analogamente \(\;\; \frac {P_m}{P_m+S_M} \overline {SP}=\rho_2 \)
moltiplicando le equazioni sopra per le masse Pm e SM ritroviamo i valori di partenza:
\(\quad \frac {S_M\ P_m}{P_m+S_M} \overline {SP}=\rho_1\ P_m \;\;\) e \(\;\;\frac {P_m\ S_M}{P_m+S_M} \overline {SP}=\rho_2\ S_M \;\;\) dove i primi membri coincidono.
Il problema dunque, note le masse, si riduce alla ricerca del valore SP, ma si osservi che SP di Fig.1B è anche dato dalla somma dei due valori \(\;\; \overline {SP}=\vec R+\vec r \;\;\), per cui
\(\quad \overline {SP}=\rho_1+\rho_2=\vec R+\vec r \;\;\): nella "Prima Legge del Moto dei Pianeti" già vista, al punto (B) del "Il Teorema dei Pianeti" si è calcolato il valore della distanza SP tramite i valori \(\;\; (\vec R+\vec r) \).
La posizione del CM' lungo la congiungente S e P è data da \(\;\; X_M=\frac {x_P P_m+x_S S_M}{P_m+S_M} \;\;\) e \(\;\; Y_M=\frac {y_P P_m+y_S S_M}{P_m+S_M} \;\;\) essendo P(xP;yP) e S(xS;yS) ottenendo le coordinate del punto CM'(XM;YM): vedi Articolo e Applet in Moto del Centro di Massa
Nella Prima Legge del Moto dei Pianeti - Moto Orbitale abbiamo trattato del Moto di Rivoluzione di due Corpi che qui riaccenniamo: in Fig.1B il Pianeta P e il Pianeta S - che abbiamo supposto essere il Sole - entrambi ruotano intorno al Centro di Massa CM e centro del riferimento cartesiano, ma il moto di S essendo molto lento rispetto all'altro Pianeta, lo abbiamo supposto immobile, per cui P passerà una volta vicino (Pe) e una volta lontano (Af), a cadenza fissa, dal punto S. La traiettoria di P rispetto a CM è una circonferenza e la sua velocità angolare è \(\;\; \omega=\frac{dE}{dt} \;\;\) ed il suo vettore velocità sarà \(\;\; \vec v=\vec\omega\times \vec R \;\;\) lungo tutta la circonferenza.
Facciamo alcune considerazioni:
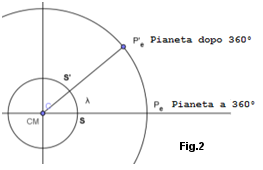
Orbita dopo 360°.Abbiamo considerato fermo il punto S (supposto il sole, ma S può rappresentare anche qualunque altro Pianeta) mentre in effetti fermo non lo è. Ciò vuol dire che quando il punto P ha percorso 360° e ritorna al punto di partenza in Pe il sole si è spostato in un punto S' e quindi il punto P dovrà percorrere ancora un tratto fino a Pe' per ritrovare l'allineamento con S, come vediamo in Fig.2. E' ovvio che la partenza della nuova rivoluzione di P, rispetto allo stesso punto S, inizierà da Pe'. Leggere: I Pianeti Dopo 360° .
Traiettoria Sole-Luna e sua Velocità Areale. Se nella Fig.1B (sopra) il punto P rappresentasse la Luna ed S la Terra, sappiamo che la Luna percorrerà una circonferenza rispetto al suo CM ed una ellisse rispetto alla Terra: ma, ancora, per il "Teorema dei Pianeti" essendo il suo moto circolare avrà una traiettoria Ellittica anche rispetto al Sole e la sua Velocità Areale sarà doppia di quella del Sole. E' importante notare che il punto Sole non è vincolato al piano orbitale del pianeta essendo un qualunque punto dello spazio. Vedi Capitolo III° Il piano nello Spazio Pag.14 . Vediamolo in un grafico:
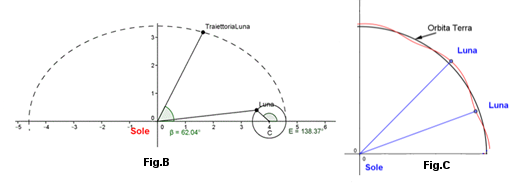
La Fig.B è l'applicazione del "Teorema dei Pianeti", e poichè la Luna si muove con la Terra la sua posizione rispetto al Sole è come in Fig.C; il Teorema ci dice solo che la distanza Sole-Luna è un vettore di Ellisse, che la velocità Areale della Luna e doppia di quella del Sole, mentre il moto della luna rispetto al Sole è quello degli Epicicli e Deferenti il cui moto è presentato, nella Geometria Parametrica come Cicloidi a Centro (Ellittica: Google "Le Cicloidi Geometria Parametrica").
Vedere l'Esempio Grafico della Traiettoria della Luna rispetto al Sole
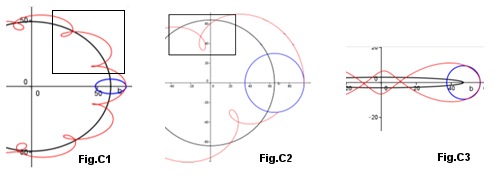
Epicicli e Deferenti. Le Fig.C1, C2 ,C3 mostrano alcune Cicloidi a Centro, sul Piano, che ben descrivono le traiettorie dei Pianeti nelle loro rivoluzioni, ricavate dall'esempio grafico degli Epicicli e Deferenti (vedi avanti) come vengono analizzate dagli studiosi. Nella Fig.C1, la Epicicloide è vista ellittica e in Fig.C2 circolare.
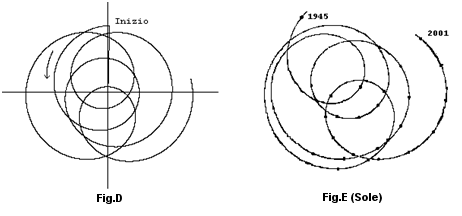
Invece la Fig.D è ottenuta come esempio, con valori a fantasia di più Epicicli, valori che possono essere mirati. Ora se prendiamo in esame la curva Fig.E delle orbite descritte dal centro del Sole, ci si accorge che la curva Figura D da noi indicata è del tutto simile.
Su una nota di F. Zagar (Astronomia Sferica e Teorica - Ed. Zanichelli 1984) su Epicicli e Deferenti, leggere: Le Cicloide a Centro in Astronomia in Articoli Esplicativi - Astronomia o come nell'esempio grafico di Fig.C su: Epicicli e Deferenti .
Da quanto detto, possiamo allora affermare che:
- le dimostrazioni fornite dalla meccanica e usate per la consueta dimostrazione delle "Leggi di Keplero" (gravitazione universale, energia potenziale, velocità areolare, ecc.) essendo le distanze, le masse, i tempi e lo stesso moto ancora quelli di una Ellisse, sono gli stessi e quindi restano valide le leggi della meccanica, che le governano;
- il CM di P, dotato di una Forza Indotta rispetto alla forza centrale S, agisce su ogni punto P della curva, per cui P ha velocità costante rispetto al suo centro massa, ma non lo ha rispetto al punto fisso S, che il Teorema dei Pianeti dimostra essere una ellisse.
Approfondimenti da Equazione Parametrica di VAG
- Argomenti nel Piano
- Capitolo VI° Pagg. 24-27: Teorema dei Pianeti
- Capitolo VII° Pag. 7: Proprietà delle Aree dell'Ellisse - In questo Capitolo si dimostra che il "Principio di costanza delle Aree dell'Ellisse" o Seconda Legge di Keplero è una proprietà valida per tutte le Ellissi
- Argomenti nello Spazio
- Capitolo III° Pag.14: Teorema dei Pianeti nello Spazio
Approfondimenti alla Prima Legge da Articoli Esplicativi - Astronomia
- Sulla Forza Centrale e Forza Centrale Indotta
- dove nella Prima Parte si ipotizza l' esistenza e l' intensità di una Forza Indotta in un qualunque punto C, rispetto ad un altro punto P di una curva chiusa
- nella Seconda Parte si analizza l'interazione di tre Punti-massa che interagiscono tra loro e quale sia l'equazione che dobbiamo applicare per una corretta interpretazione di essa
- Le Cicloidi a Centro in Astronomia
- è l'interpretazione Geometrica degli "Epicicli e Deferenti"