Considerazioni sulla Seconda Legge sul Moto dei Pianeti

---

Sappiamo dalla fisica che un corpo viaggia nello spazio secondo una parabola: la Geometria Parametrica offre interessanti indicazioni sulla equazione della parabola che ci permette lo studio di tale moto.

Moto Verticale L'unione di un moto sinistrorso di una circonferenza e di un moto perpendicolare ad essa è una parabola, del tipo \( (p-y)^2=x^2+y^2\) aperta in basso: moti che la Geometria Parametrica rappresenta entrambi come nella Fig.3, con l'Equazione del Moto degli Asteroidi (parabola con il fuoco nell'Origine - vedi sotto Approfondimenti):

Analizziamo la parabola Fig.3 creata da un corpo che si allontana dalla circonferenza di partenza lungo la direzione e verso del suo raggio (vedi: www.Geometria Parametrica CAP. III BIS - PERPENDICOLARE ALLA TANGENTE DELLA PARABOLA - CAP. VIII BIS CICLOIDI DI VAG Ellisse, Parabola, Iperbole)

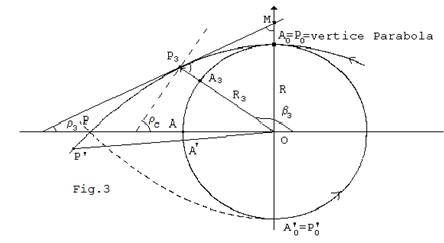
La Geometria Parametrica tra le altre cose ci dice (vedi sotto in Approfondimenti Articolo: Altezza Gittata e Velocità di Fuga):

1. posto i raggi R=0P₀ e R₃=0P₃ abbiamo  P₃A₃=A_oM e OP₃=OM e il parametro Parabola OP=p=2R .
2. \(\;\;(180-\beta_3)+\rho_c=90\;;\quad(\beta_3-90)=\rho_c\;;\quad\;\;\hat M=(90-\rho_3) \\ \quad\;\;\;\;( \beta_3-90)=\rho_c=\rho_3+(90-\hat M)=2\rho_3\quad (retta \, \rho_c\ \perp\ R_3) \)
3. nel punto P₃ la parabola vale per definizione \(\;\;OP_3=R_3=(p-y_3); \;\; p=y_3+R_3 \) p=parametro Parabola
4. il valore dell'ordinata \(\;\; y_3=R_3\sin\beta_3=R_3\sin(90+2\rho_3)=R_3\cos2\rho_3=R_3 \cos \rho_c \)
5. la differenza o altezza \(\;\; h=\overline {A_3P_3}= \overline{A_oM}=R_3-R \) (la circonferenza in 0 di raggio R₃ passa per P₃ e M)
6. il parametro della parabola per definizione (da 1.e3.):  \( \\p=\overline {OP}=2R=y_3+R_3= R_3(1+\sin\beta_3)=R_3(1+\sin(90+2\rho_3))=\\\quad \quad R_3(1+\cos2\rho_3)=2R_3\cos^2\rho_3 \)
7. essendo\(\;\;\frac {dy}{dx}=\tan \rho=-\frac {x}{p}; \;\; x_3=-p\tan\rho_3 \) dalla 6.  ( l'ascissa negativa  per il verso antiorario) \(\;\; x_3=-(2R_3\cos^2 \rho_3) \tan\rho_3=-2R_3\cos\rho_3 \sin\rho_3 =-R_3\sin2\rho_3=\\ \quad\; \quad\; \quad\; \quad=R_3\;\cos(90+2\rho_3)=R_3\cos\beta_3;\;  \quad (\beta_3-90)=2\rho_3     \)

dalla 4. e 7. abbiamo le circonferenze \(\;\; \begin{cases}-R_3\sin2\rho_3=-R_3\sin\rho_c =R_3\cos\beta_3=x_3\\ R_3\cos2\rho_3=R_3\cos\rho_c =R_3\sin\beta_3=y_3\end{cases} \) \(\;\; ( \tan\rho_c\) = tangente in P₃ della circonferenza di R₃ ).

dall'ultima della 6. abbiamo \(\;\;R=R_3\cos^2\rho_3\quad \) [A]

che assieme alla 5. da \(\;\; h=R_3-R=R_3-R_3\cos^2\rho_3=R_3\sin^2\rho_3\quad \)

e il sistema\(\quad \begin{cases}R_3\sin^2\rho_3=h\\ R_3\cos^2\rho_3=R\end{cases}\; \)dividendo avremo  \(\;\;h=R\tan^2\rho_3\quad \)  [B]

LA VELOCITA:

Posto \(\;V_3^2=\frac{Gm_1}{R_3}\;con\;R_3=\frac{V_3^2} {g_3} \;\;    \)  ( con \(\frac{Gm_1}{R_3^2} = g_3\) = gravità superficiale del relativo Pianeta, rappresentato in figura dalla circonferenza di raggio R₃ per il punto P₃) 

• Altezza di un punto P₃: \(\;\;h= A_3P_3= R \tan^2\rho_3=R_3\sin^2\rho_3=\frac {V_3^2 \sin^2 \rho_3} {g_3} \;\;\) da [B] 
• Altezza  su ordinata da 4. : \(\;\; y_3=R_3 \cos2\rho_3=R_3\sin\beta_3\;\)
• la Gittata su ascissa da 7.: \(\;\; x_3=-R_3 \sin2\rho_3=- \frac { V_3^2 \sin2 \rho_3} {g_3} =+ \frac { V_3^2 \cos \beta_3} {g_3}\;\;   \) sul riferimento oppure arco\(\; A_0A_3\)  . 
•  

• La formula che dà la Velocità Circolare alla distanza (R+h) sappiamo essere:

  \(\quad V_c=\sqrt{\frac{GM}{R+h}} \;\;\) e con \(\;\;h=R\tan^2\rho_x \;\;\) da   [B]   sarà

  \( \quad V_c=\sqrt{\frac{GM}{R}\frac{1}{1+tan^2\rho_x}}=\sqrt{\frac{ GM}{R/ \cos^2\rho_x}}=\sqrt {\frac{GM \cos^2\rho_x }{R}}= \sqrt{R g \cos^2\rho_x}\quad \) (g = gravità superficiale)   (*)

•  in (R+h) per \(\;\; \rho_x=0 \;\;\) sarà  h = 0 e quindi per \(\;\;V_c=\sqrt{\frac{GM}{R}}=\sqrt{Rg} \;\;\) Velocità al Suolo.

• per \(\;\; \rho_x=45° \;\;\) sarà  h = R  con \(\; V_p=\sqrt{\frac{GM}{2R}}=\sqrt{2R g }\quad\) velocita  nel punto P della parabola

• per \(\;\; \rho_x>45° \;\;\) sarà  h>R  e  V_F > V_P  e V_F è detta Velocità di Fuga perchè dal punto P la traiettoria di rientro della parabola non incontrerà più la circonferenza di raggio R.

• Il Periodo o Velocità di Rivoluzione è dato dalla Terza Legge di Keplero secondo quanto visto nel Moto Orbitale.

Moto Orizzontale Un generico moto parabolico con tangente in A, punto di una circonferenza, con centro nell'Origine di un riferimento cartesiano, darà luogo a parabole diverse a seconda il valore dell'angolo della tangente (detto ALZO) con il proprio Asse. Indichiamo il rapporto tra le variabili della Parabola di Vag già vista nel precedente paragrafo sulla "Seconda Legge del Moto nello Spazio" col richiamo (**):\( \quad\frac{R}{\cos\alpha_1}=\frac{R}{\cos\alpha_1} \left(1-2\cos\alpha \right) \cos\beta+\frac{R}{\cos\alpha_1}\left(\pm 2\sqrt{\cos\alpha\left(1-\cos\alpha \right)} \right)\sin\beta \;\;\):

\(\tan\rho=\frac{dy}{dx}=\frac{p}{y}=\frac{1-\cos\beta}{\sin\beta}=\sqrt{\frac{\cos\alpha}{1-\cos\alpha}}\) dove \(\cos\alpha=\frac{1-\cos\beta}{2}= \sin^2 \rho\) essendo \(\beta=2\rho\)

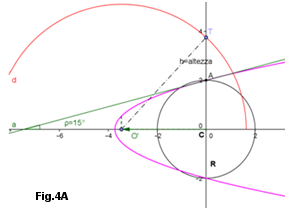
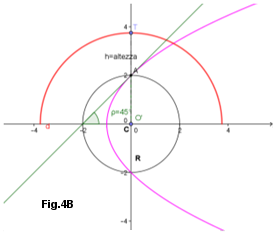
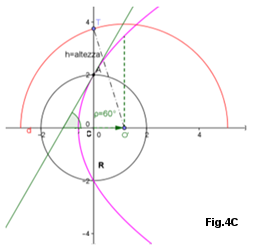
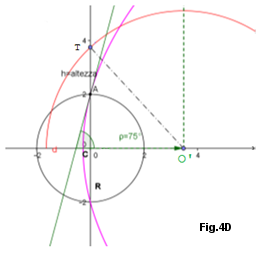
Grafici del Moto. Nelle Figure 4A,4B,4C,4D sono indicate delle Parabole aventi tangenti in A del valore \( \rho=\) 15°, 45°, ecc. L'Equazione Parametrica della Parabola, nella formula indicata, ci permette di convertire tale moto di parabola in un moto circolare (passante per un punto stabilito T), moto circolare il cui centro è nel fuoco della parabola stessa. Di conseguenza il suo moto parabolico diventa orbitale per effetto della I° Legge del Moto dei Pianeti e avrà, rispetto al centro O - Origine - della circonferenza di partenza, una traiettoria ellittica.

Dai grafici animati, mediante l'ALZO, dato dalla tangente in A e mediante l'altezza T, si ha il punto della variazione della parabola in circonferenza e l' eventuale impatto con la circonferenza di partenza: il punto di tale impatto può essere spostato, in ciascuna figura, variando l'altezza di T. Per l'ALZO=45°, Fig.4B, in quanto il Fuoco coincide con l'Origine le circonferenze non impattano mai, qualunque sia il valore di T. Vedere più avanti (sotto) in Approfondimenti da Equazione Parametrica di VAG - Grafici Animati per Fig.4

Invece che il valore della altezza AT, può essere dato il valore della distanza minima o massima, una sola perchè l'altra è obbligata, come si può vedere in Argomenti nel Piano - Capitolo V° e Capitolo XVII° in Approfondimenti da Equazione Parametrica di Vag.