Geometria Parametrica
Studio

Prima Legge del Moto dei Pianeti - Moto Orbitale
Come introduzione leggere: “L’Orologio di Tycho Brahe e le Leggi di Keplero – Geometria Parametrica”, dedotto dallo studio del “Teorema dei Pianeti”.
Moto di Rivoluzione
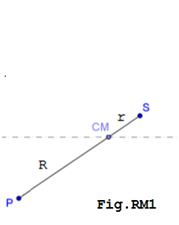
Questa espressione ci fornisce una «Tabella» di tutte le distanze SP, «simili» per i valori a quelle lasciate da Tycho Brahe in eredità a Keplero, che intuì essere quei valori raggi di ellisse. Keplero senza alcun riferimento geometrico, ipotizzò che il punto P si muovesse secondo una ellisse e il punto S ne fosse il Fuoco.Ora volendoci chiedere: se il punto P ruota secondo un moto circolare rispetto a CM, centro del riferimento cartesiano, quale è la sua traiettoria rispetto al punto massa S per ora considerato fermo?
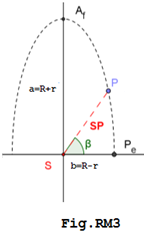
"Il Teorema dei Pianeti"
La Geometria Parametrica (che come tale non fornisce Leggi ma Teoremi) con il "Teorema dei Pianeti" : [ Cap.VI "Traslazione/Rotazione/Roto-Traslazione" da Pagg.24-27] - vedi anche "La Sintesi del Teorema" e sotto Esempio Grafico - afferma: "Data una circonferenza, ed un qualunque punto-fisso nello spazio, che non appartenga alla perpendicolare al centro di tale circonferenza, la sua distanza dai punti della circonferenza è un vettore di Ellisse, la traiettoria un Ellisse e il punto-fisso il suo centro".
(A) Dunque la traiettoria di P rispetto ad S è una ellisse i cui semi assi sono q = (R+r )=(Afelio) ed m = (R-r)= (Perielio) come vediamo nella Fig.1 sotto, nella quale il punto P (Pianeta) ruota secondo una circonferenza e la sua distanza da S (Sole) indicata da SP (la stessa cosa vale per la distanza S'P') è tale da coincidere con un valore reale lo stesso che nelle leggi di Keplero: infatti in entrambi i casi tutte le distanze sono comprese tra la distanza minima SPe e la distanza massima SAf.
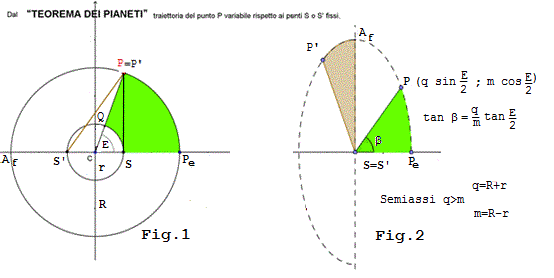
(B) La Fig.1, data dal "Teorema dei Pianeti", coincide con quella analizzata in Fig.RM1 nel Moto di Rivoluzione; invece la Fig.2 rappresenta la traiettoria del punto P, con coordinate date da Fig.1, ma coincidente con la Fig.RM3. Fatto dunque: \(\;\; \overline{SP}^2=R^2+r^2-2Rr\cos2\frac{E}{2} \;\;\) e sviluppato avremo
\(\quad \left ((R+r) \sin \tfrac {E} {2};\ (R-r)\cos \tfrac {E} {2} \right )\;\;\) quindi (vedi Fig.2) \(\;\; \left (q \sin \tfrac {E} {2};\ m\cos \tfrac {E} {2} \right )\;\;\) e la distanza
\(\quad \overline{SP}=\sqrt{q^2\sin^2\tfrac{E}{2}+m^2\cos^2\tfrac{E}{2}}=\sqrt{(R+r)^2\sin^2\tfrac{E}{2}+(R-r)^2\cos^2\tfrac{E}{2}}=\sqrt{(Afelio)^2\sin^2\tfrac{E}{2}+(Perielio)^2\cos^2\tfrac{E}{2}}\quad \) Raggio d'Ellisse
Tale "Teorema", tra le altre cose, stabilisce la corrispondenza biunivoca tra circonferenza e relativa ellisse e fornisce la soluzione del sistema a due incognite q>m e R>r : (vedi avanti "Cenni di Geometria" espressione [4]).
Per una spiegazione sintetica delle proprietà di cui sopra clicca qui Note sul Teorema dei Pianeti
Note sul Teorema dei Pianeti
Da Fig.1 e Fig.2 sopra la Geometria ci dice:
- la distanza SP e S'P' della Circonferenza sono anche vettori SP e S'P' della Ellisse - Teorema dei Pianeti
- l'area SQPPe è doppia delle aree SPPe = S'P'Af e tutte percorse nello stesso tempo
- la velocità di percorrenza di P sulla circonferenza è doppia di quella di P sull' Ellisse (metà circonferenza = un quarto della velocità di P sulla Ellisse): la qual cosa, è la dimostrazione geometrica della Velocità Areale
- i valori fisici delle distanze del punto P dal Sole sono compresi tra il Perielio e l'Afelio
- essendo la traiettoria di P nei confronti di S una ellisse, ed S centro di tale ellisse, la sua velocità andrà calcolata sulla ellisse, potendosi ora considerare S punto di una Forza Centrale. Ora,la velocità del punto P rispetto al suo CM è un valore fisico reale, in quanto riferita ad una reale circonferenza e non ad una traiettoria, ma quando il punto P ruota intorno ad S avvengono due cose:
- la Velocità Areale è costante nel tempo (di P su CM, doppia di quella di P su S)
- la variabilità delle distanze di P da S
- questi due valori si quantificano nella traiettoria Ellittica di P su S, dando nell'ellisse velocità diverse da quelle ottenute da P nella circonferenza. Nel punto Pe dove il punto P della circonferenza coincide con quello della traiettoria ellittica, la velocità \( \vec v=\vec\omega \times R \) sulla circonferenza diventa \( \vec v=\vec \omega \times (R-r)=\vec \omega \times m\;\) (m = asse) oppure se siamo in S' (vedi Fig.1-2) \(\;\; \vec v=\vec \omega \times (R+r)=\vec \omega \times q \;\) (q = asse) la cui semi somma delle due velocità, è appunto \( \vec v=\vec\omega \times R \).
- gli archi dei quadranti della circonferenza di raggio R e della relativa ellisse hanno perimetri uguali (non i settori intermedi)
-
la stessa Terza Legge di Keplero, vedi più avanti, trova una sua logica collocazione dove per R = raggio della circonferenza abbiamo:
\(\quad V=\sqrt{\frac{GM} {R}}=\sqrt{\frac{2GM}{q+m}}=\frac{(q+m)\pi}{T}\)
Tale velocità è la velocità media ed è la stessa nella circonferenza e nell'ellisse, nel primo caso essa è data dalla velocità angolare con moto circolare uniforme e come tale è confermata dalla formulazione di Newton, nell'ellisse invece, come visto al punto 6. essendo il valore dell'arco di circonferenza diverso da quello dell' ellisse la velocità dell'arco di quest'ultima è diversa, come ci indica il valore geometrico del Perimetro dell'Ellisse, con l'Integrale Ellittico di 2° specie, in forma parametrica:
\(\quad s=\int_ {o}^{\frac {\pi}{2}} \sqrt {q^2\sin^2 E+m^2 \cos^2E}\;dE=\int_ {o}^{\frac {\pi}{2}} \sqrt {R^2+r^2 -2R rcos2E} \;dE \)
-
Dunque le parziali velocità circolare del punto P, costante rispetto al polo CM di Fig.RM2, è diversa dalla sua velocità ellittica rispetto al punto S di Fig.RM3, tuttavia la somma di queste velocità sarà la velocità media indicata in 8. Con riferimento al Moto di Rivoluzione (Fig.RM1) con Af = q = asse-maggiore e Pe = m = asse-minore indichiamo le distanze, già viste sopra: \(\quad \overline{SP}=\sqrt{\tfrac{1}{2}\left[A_f^2(1-\cos E)+P_e^2(1+\cos E)\right] } \;\;\) e l'arco di ellisse: \(\quad s=\int_ {o}^{\frac {\pi}{2}} \sqrt {\tfrac{1}{2}\left[A_f^2(1-\cos E)+P_e^2(1+\cos E)\right] }\;dE=\int_ {o}^{\frac {\pi}{2}} \sqrt {A_f^2\sin^2 \frac{E}{2}+P_e^2 \cos^2\frac{E}{2} }\;dE \).
Il Moto di Rivoluzione e il Teorema dei Pianeti
Avendo ipotizzato che il "Teorema dei Pianeti" coincida con il Moto di Rivoluzione dei Pianeti allorquando il suo centro di riferimento coincide col Centro di Massa del moto dei due Pianeti, e la massima distanza (Afelio) e la minima (Perielio) sono in linea.
Il caso in esame è una semplificazione che considera il Moto di Rivoluzione delle due masse complanari. In realtà il "Teorema dei Pianeti" ci dice che le traiettorie ellittiche avvengono allo stesso modo allorquando il punto massa, considerato fermo, è un qualunque punto fuori dal piano dell'orbita circolare dell'altro - caso Luna (Orbita Circolare) Sole (Punto Fermo) e la sua traiettoria ellittica.
Se volessimo applicare alle formule, ottenute dal "Teorema dei Pianeti", i dati relativi al moto di rivoluzione dei Pianeti, abbiamo che le distanze Af = Afelio e Pe = Perielio sulla circonferenza, danno dalla Fig.RM2 e Fig.RM3:
\(\quad R=\frac{A_f+P_e}{2} \;\;\) e \(\;\; r=\frac{A_f-P_e}{2}\)e per il "Teorema dei Pianeti": \(\;\; \begin{cases}A_f=(R+r)=a \\ P_f=(R-r)=b \end{cases} \;\;\) dove a>b sono i semiassi dell'Ellisse [7]
Distanza di un Pianeta da un Punto Fisso (Sole).
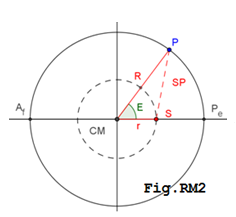
Dalla Fig.RM2 vista, abbiamo che:
\(\quad \overline{SP}=\left| \sqrt{R^2+r^2-2Rr\cos E}\right| \;\;\) applicando poi la [7] otteniamo:
\(\quad \overline{SP}=\sqrt{\tfrac{1}{2}\left[A_f^2(1-\cos E)+P_e^2(1+\cos E)\right]} \;\;\) Raggio di Ellisse [7bis]
che per E=0° è SP=Pe(Perielio) e per E=180° è SP=Af (Afelio); sviluppiamo la [7bis] ponendo:
\(\;\;\sin^2 \frac{E}{2}=\frac{(1-\cos E)}{2} \quad \cos^2 \frac{E}{2}=\frac{(1+\cos E)}{2} \)
\(\quad \overline{SP}^2 =A^2_f \sin^2\frac{E}{2}+P^2_e \cos^2\frac{E}{2}\) \(\;\; \begin{cases}\overline{SP} \sin\beta=A_f\sin\frac{E}{2} \\ \overline{SP} \cos\beta=P_e\cos\frac{E}{2} \end{cases} \qquad SP=A_f\sin E/2 \sin\beta+P_e\cos E/2 \cos\beta \)
che sappiamo essere una Ellisse per \(\tan\beta=\frac{A_f}{P_e} \tan \frac{E}{2}\)
Dal "Teorema dei Pianeti" abbiamo che ogni distanza SP calcolata sulla circonferenza è un raggio di ellisse determinata dal valore E/2 che giustifica sia la Velocità Areale doppia sulla circonferenza di quella corrispondente dell'ellisse, sia Afelio e Perielio come assi.
Vedere l'Esempio Grafico del Teorema dei Pianeti
Nel caso specifico l'espressione [7bis] dà la distanza di un Pianeta dal Sole, determinata dalla Anomalia E di Fig.RM2 al tempo t1.
Avendo una soluzione al problema prettamente Geometrico non sono state discusse le considerazioni analitiche dovute a Tempo, Velocità, Accelerazione, Massa, ecc. per cui rimangono valide le soluzioni analitiche delle Leggi di Newton.
Ad esempio da Newton sappiamo che la forza di attrazione tra due Pianeti è indicata con \(\;\;F=G\frac{m_1 m_3}{r^2}\) (G = Costante di Gravitazione Universale) al tempo t1, che ora possiamo indicare con \(\;\;F_{t_1}=G\frac{m_1 m_2}{SP^2} \;\;\) e tale risultato concorda con La Terza Legge di Keplero (Vedere più avanti).
Cenni di Geometria
Da la "Geometria Parametrica - Equazione Parametrica di Vag".
\(\quad \begin {cases} \left|OA \right|\cos\beta=x \\\left|OA \right|\cos\gamma=y \end{cases}\quad \) \(\left|OA \right|=\sqrt{x^2+y^2}\quad\) \(cos^2\beta+cos^2\gamma=1 \)
Mediante l’Equazione di Vag. l’Ellisse è rappresentata da:
\(\quad \begin {cases} \left|OA \right|\cos\beta=x=a\cos\alpha \\\left|OA \right|\sin\beta=y=b\sin\alpha \end{cases} \quad\) \( \overline{OA}=(a\cos\alpha)\cos\beta+(b\sin\alpha\sin\beta ) \;\;\) [2]
a > b = semiassi per 0° < \(\alpha\)< 360°. Relazione tra a e b nell’Ellisse: \(\;\; \tan\beta=\frac{b}{a} \tan\alpha \;\;\) [3]
Dati due numeri a>b \(\in R^+\) ne esistono altri due R e r che possono essere posti in relazione biunivoca secondo il seguente sistema:
\(\quad \begin{cases} a=R+r\\ b=R-r \end{cases} \iff \begin{cases} R=\frac{a+b}{2}\\r=\frac{a-b}{2}\end{cases} \;\;\) [4]
e se a > b sono semi-assi di una ellisse e R > r raggi di due circonferenze posso scrivere:\(\;\; 2R\pi=2\frac{a+b}{2}\pi\)
L'espressione sopra si collega perfettamente all'esempio empirico:
«Se prendo un anello (di metallo ad esempio) e lo stringo su due poli, l'anello si allarga assumendo la forma di una ellisse e più stringo più si allarga. Notiamo che l'area originaria della circonferenza tende a zero se continuiamo a stringere, mentre il suo perimetro rimane sempre uguale a quello dell' anello iniziale».
Dunque il perimetro dell'anello di raggio R e dell'ellisse è uguale (non i valori intermedi), come ci indica la relazione [4], e la stessa Trasformazione Affine di una circonferenza in ellisse, confermata dal valore geometrico del Perimetro della Ellisse, con l'integrale di 2° specie, dove per \(\;\;\frac{\pi}{2} \) è \(\;\; R=\frac{a+b}{2}\; \;\;\) con a > b semi assi dell'ellisse Nota (*) [4bis]
La [4] e la [4bis] sono suffragate anche dal "Teorema dei Pianeti" e dall'Esempio Grafico (vedi sopra) che, lega in una relazione biunivoca geometrica la circonferenza e la relativa ellisse e viceversa, e per il Moto di Rivoluzione \(\;\; R=\frac{A_f+P_e}{2}\).
La Terza Legge di Keplero
La terza Legge di Keplero è sintetizzata dalla formula:
\(\quad \frac{a^3}{T^2}=K=costante \;\;\) [1]
con T = periodo e a = semi-asse maggiore di una ellisse, che essendo una costante, è presentata come raggio di una circonferenza: da tale condizione Newton mosse per la sua dimostrazione analitica alla condizione di essere in presenza di una orbita circolare, di una velocità orbitale costante e di un moto circolare uniforme Nota= (*).
Più esplicitamente scriviamo la Velocità Orbitale Media \(\quad\frac{2\pi R}{T}=V\) ma \(V=\sqrt{\frac{GM}{R}} \;\;\) [2]
con significato noto T = periodo R = raggio di una circonferenza e con rapidi passaggi abbiamo:
\(\quad\frac{R^3}{T^2}=\frac{GM}{2^2 \pi^2}=costante \;\;\) [3]
La formula [1] e [3] hanno lo stesso significato, quando si pone a = R ma dovendoci rifare non ad una circonferenza ma ad una ellisse dovrò scrivere secondo la [2]:
\(\quad\frac{Perimetro Ellisse}{T}=V \)
che in [4bis] di Cenni di Geometria il valore del perimetro dell'ellisse è dato sostituendo \(\;\; R=\frac{a+b}{2}\).
Allora posso scrivere la [3]:
\(\quad \frac{(a+b)^3}{2^3 T^2}=\frac{GM}{2^2 \pi^2} ; \;\; \frac{(a+b)^3}{T^2}=\frac{2GM}{\pi^2}=costante \;\;\) e la velocità sarà:
\(\quad V=\sqrt{\frac{GM}{R}}=\sqrt{\frac{2GM}{(a+b)}}=\frac{(a+b)\pi}{T} \;\;\) [4]
l'ultima espressione è, geometricamente come quella di partenza riferita questa volta ad una circonferenza di eguale perimetro dell'ellisse (giusto l'esempio empirico [4bis] di Cenni di Geometria).
Tenendo presente le considerazioni viste in Il Moto di Rivoluzione e il Teorema dei Pianeti riscriviamo la [4] riferendoci al loro Af = Afelio e Pe = Perielio:
\(\quad \frac{(A_f+P_e)^3}{2T^2}=K=costante\) \(\;\; V=\sqrt{\frac{2GM}{(A_f+P_e)}}=\frac{(A_f+P_e)\pi}{T} \)
che è la formula esatta da applicare per la Terza Legge di Keplero e \(\;\; 2R\pi=(A_f+P_e)\pi \;\;\) per calcolare il perimetro di una Ellisse.
La velocità indicata in [4] è la Velocità Media.
Come Circonferenza è data dalla velocità angolare con moto circolare uniforme, e quindi la formulazione di Newton a cui ci si riferisce è esatta, perché siamo effettivamente in presenza di una circonferenza di eguale perimetro di una ellisse.
Come Ellisse la velocità media complessiva è uguale ma come indica l'Esempio nel capitolo relativo al calcolo del perimetro dell'ellisse Nota (**), sono uguali solo gli archi dei rispettivi quarti (\(= \frac{\pi}{2}\)), e differenti gli archi riferiti agli angoli dei valori intermedi (\(< \frac{\pi}{2}\)), è ovvio che la somma delle velocità medie parziali nell'ellisse darà la Velocità Media calcolata per entrambe le figure.
Esempi
- Il Perimetro di un Pianeta
- Distanza dei Pianeti dal Sole - Confronto
Summa
Avendo fornito al problema una soluzione prettamente geometrica con i Pianeti come punti-massa, non sono state discusse le considerazioni analitiche dovute a Tempo, Velocità, Accelerazione, Massa, ecc. per cui rimangono valide le soluzioni analitiche delle leggi di Newton; si deve allora considerare che l'equazione differenziale del moto dei corpi celesti, integrata,la quale indica appunto una conica, che nella nostra tesi è data da una ellisse, non collegata alla reale posizione dei Pianeti nello Spazio.. Tale ellisse, sviluppata dal “Teorema dei Pianeti” ha come riferimento solo il valore delle distanze SP, con S centro e P punto del perimetro e i cui valori sono per il Moto di Rivoluzione: a=Af e b=Pe semi-assi ellisse; β angolo al centro.
D'altra parte le leggi di Newton spiegano l'interazione tra due masse, ma non spiegano il moto e la posizione di ciascuna di esse nello spazio, problema che si è voluto risolvere ponendo arbitrariamente il Sole nel punto-fuoco di una ellisse.
Si osservi che tutte le considerazioni sui Pianeti sono state fatte considerando ogni corpo celeste come punto-massa, punto che può essere fisicamente identificato con il centro del Pianeta. E' tale punto che ruota secondo una circonferenza di centro CM. Mentre un qualunque punto della superficie del Pianeta, ruotando rispetto al suo centro di rotazione CR ruoterà rispetto a un qualunque altro punto, per lo stesso "Teorema dei Pianeti", secondo una traiettoria ellittica.
L'insieme di tali considerazioni liberano il moto dei Pianeti da certe limitazioni semplicemente assurde, giustificando appieno la:
I° Legge del Moto dei Pianeti - Moto orbirale
I Pianeti ruotano secondo Orbite Circolari e tutti, uno rispetto all'altro, secondo traiettorie Ellittiche.Note
- (*) Infatti applicando la [1] e considerando l'area in funzione del tempo \(\;\; \frac{dA}{dt}=\frac{1}{2}a^2\frac{dE}{dt}=\frac{1}{2}a \omega \;\;\) ecc. Newton dimostra che la Forza esercitata dal Sole su un Pianeta, è inversamente proporzionale al quadrato della distanza e l'unica forza agente è la centripeta \(\;\; F_c=\left(\frac{4 \pi^2}{K} \right) \frac{m}{a^2} \;\;\) dove a= \( \frac{a+b}{2} \)=costante, diventa raggio della biunivoca circonferenza.
- (**) Geometria Parametrica - Cap.VII "Area e Perimetro Ellisse" Pag.12-13