Le Curve di Vag e Bezier

---

Nel costruire una curva la domanda che dobbiamo porci è quali siano gli elementi che determinano la curva stessa.

L'idea di Bezier di cercare di costruire una curva mediante punti seguendo l'andamento di un poligono di controllo, può servire per sviluppare questa ricerca, che può essere interpretata anche mediante la Geometria Parametrica.

 Teoria delle Curve di VAG.

Il Cap. I della Geometria Parametrica ci illustra il significato di Equazione Parametrica di VAG a cui ci rifacciamo nel presente scritto, per cui un segmento OA di angolo ß, preso come la distanza dei due estremi O ed A, sul piano ed in un riferimento cartesiano sappiamo potersi, anche scrivere nella forma:

\(\begin{cases} \overline{OA}\cos\beta =x \\ \overline{OA}\sin\beta =y \end {cases} \qquad \left| \overline{OA} \right| =x\cos\beta+y\sin\beta\)

Richiamandoci ai concetti di Bezier possiamo anche considerare il segmento OA come un infinito numero di punti che si susseguono da O ad A mantenendo sempre una determinata direzione e verso che nel nostro caso è determinato dalla costanza di ß.

Va da sé che facendo la somma di \(\overrightarrow{OA t}\quad t\in (0,1)\) in base all'incremento di t, avremo la conta dei punti che formano il segmento OA e se noi, con la Geometria Parametrica, poniamo \(t= \sin\alpha\ oppure\ t=\cos\alpha \quad per \quad 0°\le \alpha \le\ 90°\) avremo il tracciato di un segmento OA per punti: a crescere per t = sinα (da O verso A), a decrescere per t = cosα (da A verso O).

Nell'Equazione Parametrica di VAG un tale segmento orientato per punti si esprime tramite ß, con:

\(\begin {cases} \left(\overline {OA}\sin\alpha \right) \cos\beta=x\sin\alpha \\ \left(\overline {OA}\sin\alpha \right) \sin\beta=y\sin\alpha \end{cases} \qquad \left( \overline {OA} \sin\alpha \right)=(x\sin\alpha)\cos\beta+(y \sin\alpha) \sin\beta\)

Poiché un qualunque valore del tipo \(\overline{OA}^2 =x^2+y^2\) può essere considerato \(\left( \overline {OA} \sin\alpha \right)^2=(x\sin\alpha)^2+(y \sin\alpha)^2\) vuol dire che ogni linea o curva può essere sempre considerata - nella nostra fattispecie - come una poligonale di punti allorquando α sia sufficientemente frazionato.

Tale affermazione vale sia per il segmento OA come per le coordinate x e y a loro volta formanti una poligonale puntuale. Si osservi l’Equazione Parametrica di VAG della figura 05:

\(\mathbf{(1)} \; \begin {cases} \left(\overline {OA}\sin\alpha \right) \cos\beta=q\sin\alpha \\ \left(\overline {OA}\sin\alpha \right) \sin\beta=m\sin\alpha \end{cases}\)

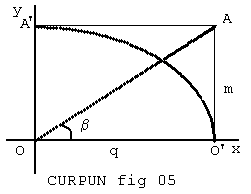
dove avendo segmentato sia OA che q ed m; questa equazione, ci darà ancora un segmento OA per punti. La prima variazione che posso apportare è sostituire sinα con cosα ed avere:

\(\mathbf{(2)} \; \begin {cases} \left(\overline {OA}\cos\alpha \right) \cos\beta=\left(\overline {OA}\cos\beta \right) \cos\alpha=q\cos\alpha \\ \left(\overline {OA}\sin\alpha \right) \sin\beta=\left(\overline {OA}\sin\beta \right) \sin\alpha=m\sin\alpha \end{cases}\)

che non è più una Equazione di VAG, e che mi dà ancora la stessa segmentazione di OA ma che ora traccia una curva O'A' in cui ogni punto ha valore e direzione ß costanti, infatti la curvatura è data dalla differenza tra ascissa e ordinata, tra m e q e non dal valore di ß che è costante e dato da \(\tan\beta=\frac{m}{q}\); per m=q si avrebbe un arco di circonferenza.

Possiamo allora dire che se un generico segmento OA può essere segmentato per punti, ci permette di fare le seguenti considerazioni:

1. 1 Se ogni punto del segmento OA può essere orientato per il valore di ß, variando ß ad ogni punto non avrò più un segmento tipo OA per punti ma un segmento-curva per punti. L’esempio più semplice è variare per ogni punto di OA l’angolo facendo (ß sin α):

   \(\mathbf{(3)} \; \begin {cases} \left(\overline {OA}\sin\alpha \right) \cos(\beta\sin\alpha)=x \\ \left(\overline {OA}\sin\alpha \right) \sin(\beta\sin\alpha)=y \end{cases}\) come mostrato in figura 20.

   

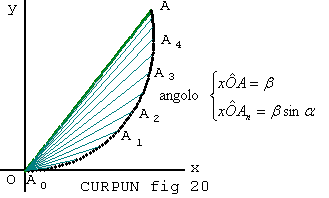
   è ovvio che potrei sostituire (ß sin α) con un valore appropriato che cambierebbe la figura. Si osservi che avendo generalizzato le coordinate x ed y la (3) è una Equazione Parametrica di VAG, per \(\overline {OA}^2\sin^2\alpha=x^2+y^2\)

2. 2 Se in (3) sostituiamo (ß sin α) con (ß sin tα) al variare di t si avrebbero altre figure come indicato in figura 22;

   

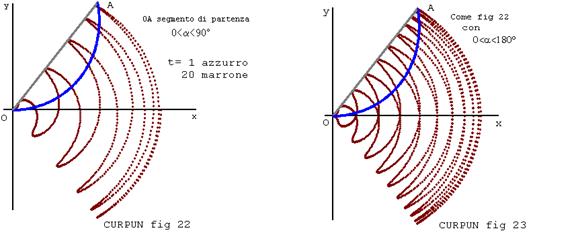
   mentre nella figura 23 il valore α e fatto compreso tra \(0°\le\alpha\le90°\) che dà la stessa figura di fig. 22 raddoppiata. In entrambi i casi è stato usato il programma TEO-CURVE SEG-PUNTO , incrementando α con il valore 0,1;

   

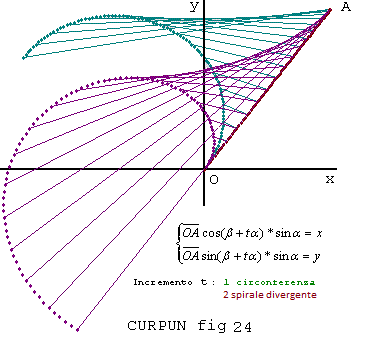
   Nella figura 24 abbiamo incrementato sommando all’angolo ß l’angolo tαed ottenuto le figure relative.

3. 3 Se il valore (OA sin α) per \(0°\le\alpha\le180°\) è la somma di elementari segmenti di OA presi come punto, possiamo dunque considerare (OA sin α) come accennato all’inizio, una poligonale di segmenti-punto opportunamente allineati.

   Mentre abbiamo anche visto che variando ß, angolo del segmento OA, possiamo dare una direzione e verso ad ogni segmento-punto, ed avere in tal caso una poligonale di segmenti-punto non più allineati, cioè una curva.

4. 4 Se (OA sin α) è un insieme di punti che si sommano possiamo allora prendere in considerazione un singolo segmento-punto ε e orientarlo per un ß appropriato.

---

 Creazione di una Curva

1. Se la curva è data da una equazione essa può essere tracciata, per direzione e verso, tramite un ß dato dall'angolo della tangente in ogni suo segmento-punto:l'esempio più immediato, di tale tracciamento, è quello di una Circonferenza tracciata senza ricorrere al valore del suo raggio come si vede in Fig.24 e meglio nel riquadro di seguito, in "Curve note tracciate per punti di tangente".
2. Se la curva è un disegno può essere ricalcata usando un opportuno numero di segmenti corda per essere ricostruita.

Tenendo conto di tutto ciò che abbiamo fin qui illustrato proviamo a creare una curva partendo da un segmento AB: una curva che parta da A e finisca in B: poichè tale curva è pur sempre data dal valore dell'ascissa e dell'ordinata del segmento AB, agiremo su questi due elementi, incrementando e decrementando gli angoli che governano tutti i segmenti-punto di questi due valori (come indicato nella prima parte).

Il programma che presentiamo è uno dei possibili programmi che si possono studiare per creare una curva ragionata: esso si rifà ai concetti propri della Geometria Parametrica e fornisce delle indicazioni che sono una delle tante interpretazioni di cui possiamo avvalerci per ottenere una curva.